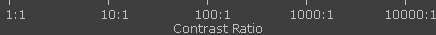DYNAMIC RANGE IN DIGITAL PHOTOGRAPHY
Dynamic range in photography describes the ratio between the maximum and minimum measurable light intensities (white and black, respectively). In the real world, one never encounters true white or black — only varying degrees of light source intensity and subject reflectivity. Therefore the concept of dynamic range becomes more complicated, and depends on whether you are describing a capture device (such as a camera or scanner), a display device (such as a print or computer display), or the subject itself.

Just as with color management, each device within the above imaging chain has their own dynamic range. In prints and computer displays, nothing can become brighter than paper white or a maximum intensity pixel, respectively. In fact, another device not shown above is our eyes, which also have their own dynamic range. Translating image information between devices may therefore affect how that image is reproduced. The concept of dynamic range is therefore useful for relative comparisons between the actual scene, your camera, and the image on your screen or in the final print.
INFLUENCE OF LIGHT: ILLUMINANCE & REFLECTIVITY
Light intensity can be described in terms of incident and reflected light; both contribute to the dynamic range of a scene (see tutorial on "camera metering and exposure").


Scenes with high variation in reflectivity, such as those containing black objects in addition to strong reflections, may actually have a greater dynamic range than scenes with large incident light variation. Photography under either scenario can easily exceed the dynamic range of your camera — particularly if the exposure is not spot on.
Accurate measurement of light intensity, or luminance, is therefore critical when assessing dynamic range. Here we use the term illuminance to specify only incident light. Both illuminance and luminance are typically measured in candelas per square meter (cd/m2). Approximate values for commonly encountered light sources are shown below.
Here we see the vast variation possible for incident light, since the above diagram is scaled to powers of ten. If a scene were unevenly illuminated by both direct and obstructed sunlight, this alone can greatly increase a scene's dynamic range (as apparent from the canyon sunset example with a partially-lit cliff face).
DIGITAL CAMERAS
Although the meaning of dynamic range for a real-world scene is simply the ratio between lightest and darkest regions (contrast ratio), its definition becomes more complicated when describing measurement devices such as digital cameras and scanners. Recall from the tutorial on digital camera sensors that light is measured at each pixel in a cavity or well (photosite). Each photosite's size, in addition to how its contents are measured, determine a digital camera's dynamic range.
 Black Level
Black Level(Limited by Noise)
 White Level
White Level(Saturated Photosite)
 Darker White Level
Darker White Level(Low Capacity Photosite)
Photosites can be thought of as buckets which hold photons as if they were water. Therefore, if the bucket becomes too full, it will overflow. A photosite which overflows is said to have become saturated, and is therefore unable to discern between additional incoming photons — thereby defining the camera's white level. For an ideal camera, its contrast ratio would therefore be just the number of photons it could contain within each photosite, divided by the darkest measurable light intensity (one photon). If each held 1000 photons, then the contrast ratio would be 1000:1. Since larger photosites can contain a greater range of photons, dynamic range is generally higher for digital SLR cameras compared to compact cameras (due to larger pixel sizes).
Technical Note: In some digital cameras, there is an extended low ISO setting which produces less noise, but also decreases dynamic range. This is because the setting in effect overexposes the image by a full f-stop, but then later truncates the highlights — thereby increasing the light signal. An example of this is many of the Canon cameras, which have an ISO-50 speed below the ordinary ISO-100.
In reality, consumer cameras cannot count individual photons. Dynamic range is therefore limited by the darkest tone where texture can no longer be discerned; we call this the black level. The black level is limited by how accurately each photosite can be measured, and is therefore limited in darkness by image noise. Therefore, dynamic range generally increases for lower ISO speeds and cameras with less measurement noise.
Techncal Note: Even if a photosite could count individual photons, it would still be limited by photon noise. Photon noise is created by the statistical variation in arrival of photons, and therefore represents a theoretical minimum for noise. Total noise represents the sum of photon noise and read-out noise.
Overall, the dynamic range of a digital camera can therefore be described as the ratio of maximum light intensity measurable (at pixel saturation), to minimum light intensity measurable (above read-out noise). The most commonly used unit for measuring dynamic range in digital cameras is the f-stop, which describes total light range by powers of 2. A contrast ratio of 1024:1 could therefore also be described as having a dynamic range of 10 f-stops (since 210 = 1024). Depending on the application, each unit f-stop may also be described as a "zone" or "eV."
SCANNERS
Scanners are subject to the same saturation:noise criterion as for dynamic range in digital cameras, except it is instead described in terms of density (D). This is useful because it is conceptually similar to how pigments create tones in printed media, as shown below.
 |
 |
 |
|
| Low Reflectance (High Density) |
High Reflectance (Low Density) |
High Pigment Density (Darker Tone) |
Low Pigment Density (Lighter Tone) |
The overall dynamic range in terms of density is therefore the maximum pigment density (Dmax), minus the minimum pigment density (Dmin). Unlike powers of 2 for f-stops, density is measured using powers of 10 (just as the Richter scale for earthquakes). A density of 3.0 therefore represents a contrast ratio of 1000:1 (since 103.0 = 1000).
| Dynamic Range of Original | |
|---|---|
| Dynamic Range of Scanner |
Instead of listing total density (D), scanner manufacturer's typically list just the Dmax value, since Dmax - Dmin is approximately equal to Dmax. This is because unlike with digital cameras, a scanner has full control over it's light source, ensuring that minimal photosite saturation occurs.
For high pigment density, the same noise constraints apply to scanners as digital cameras (since they both use an array of photosites for measurement). Therefore the measurable Dmax is also determined by the noise present during read-out of the light signal.
COMPARISON
Dynamic range varies so greatly that it is commonly measured on a logarithmic scale, similar to how vastly different earthquake intensities are all measured on the same Richter scale. Here we show the maximum measurable (or reproducible) dynamic range for several devices in terms any preferred measure (f-stops, density and contrast ratio). Move your mouse over each of the options below to compare these.
| Select Measure for Dynamic Range: | ||
|---|---|---|
| f-stops | Density | Contrast Ratio |
![]()
![]()
| Select Types to Display Above: | |||
|---|---|---|---|
| Printed Media | Scanners | Digital Cameras | Display Devices |
Note the huge discrepancy between reproducible dynamic range in prints, and that measurable by scanners and digital cameras. For a comparison with real-world dynamic range in a scene, these vary from approximately 3 f-stops for a cloudy day with nearly even reflectivity, to 12+ f-stops for a sunny day with highly uneven reflectivity.
Care should be taken when interpreting the above numbers; real-world dynamic range is a strong function of ambient light for prints and display devices. Prints not viewed under adequate light may not give their full dynamic range, while display devices require near complete darkness to realize their full potential — especially for plasma displays. Finally, these values are rough approximations only; actual values depend on age of device, model generation, price range, etc.
Be warned that contrast ratios for display devices are often greatly exaggerated, as there is no manufacturer standard for listing these. Contrast ratios in excess of 500:1 are often only the result of a very dark black point, instead of a brighter white point. For this reason attention should be paid to both contrast ratio and luminosity. High contrast ratios (without a correspondingly higher luminosity) can be completely negated by even ambient candle light.
THE HUMAN EYE
The human eye can actually perceive a greater dynamic range than is ordinarily possible with a camera. If we were to consider situations where our pupil opens and closes for varying light, our eyes can see over a range of nearly 24 f-stops.
On the other hand, for accurate comparisons with a single photo (at constant aperture, shutter and ISO), we can only consider the instantaneous dynamic range (where our pupil opening is unchanged). This would be similar to looking at one region within a scene, letting our eyes adjust, and not looking anywhere else. For this scenario there is much disagreement, because our eye's sensitivity and dynamic range actually change depending on brightness and contrast. Most estimate anywhere from 10-14 f-stops.
The problem with these numbers is that our eyes are extremely adaptable. For situations of extreme low-light star viewing (where our eyes have adjusted to use rod cells for night vision), our eyes approach even higher instantaneous dynamic ranges (see tutorial on "Color Perception of the Human Eye").
BIT DEPTH & MEASURING DYNAMIC RANGE
Even if one's digital camera could capture a vast dynamic range, the precision at which light measurements are translated into digital values may limit usable dynamic range. The workhorse which translates these continuous measurements into discrete numerical values is called the analog to digital (A/D) converter. The accuracy of an A/D converter can be described in terms of bits of precision, similar to bit depth in digital images, although care should be taken that these concepts are not used interchangeably. The A/D converter is what creates values for the digital camera's RAW file format.
| Bit Precision of Analog/Digital Converter |
Contrast Ratio | Dynamic Range | |
|---|---|---|---|
| f-stops | Density | ||
| 8 | 256:1 | 8 | 2.4 |
| 10 | 1024:1 | 10 | 3.0 |
| 12 | 4096:1 | 12 | 3.6 |
| 14 | 16384:1 | 14 | 4.2 |
| 16 | 65536:1 | 16 | 4.8 |
Note: Above values are for A/D converter precision only, and should not be used to interpret results for 8 and 16-bit image files. Furthermore, values shown are a theoretical maximum, assuming noise is not limiting, and this applies only to linear A/D converters.
As an example, 10-bits of tonal precision translates into a possible brightness range of 0-1023 (since 210 = 1024 levels). Assuming that each A/D converter number is proportional to actual image brightness (meaning twice the pixel value represents twice the brightness), 10-bits of precision can only encode a contrast ratio of 1024:1.
Most digital cameras use a 10 to 14-bit A/D converter, and so their theoretical maximum dynamic range is 10-14 stops. However, this high bit depth only helps minimize image posterization since total dynamic range is usually limited by noise levels. Similar to how a high bit depth image does not necessarily mean that image contains more colors, if a digital camera has a high precision A/D converter it does not necessarily mean it can record a greater dynamic range. In effect, dynamic range can be thought of as the height of a staircase whereas bit depth can be thought of as the number of steps. In practice, the dynamic range of a digital camera does not even approach the A/D converter's theoretical maximum; 8-12 stops is generally all one can expect from the camera.
INFLUENCE OF IMAGE TYPE & TONAL CURVE
Can digital image files actually record the full dynamic range of high-end devices? There seems to be much confusion on the internet about the relevance of image bit depth on recordable dynamic range.
We first need to distinguish between whether we are speaking of recordable dynamic range, or displayable dynamic range. Even an ordinary 8-bit JPEG image file can conceivably record an infinite dynamic range — assuming that the right tonal curve is applied during RAW conversion (see tutorial on curves, under motivation: dynamic range), and that the A/D converter has the required bit precision. The problem lies in the usability of this dynamic range; if too few bits are spread over too great of a tonal range, then this can lead to image posterization.
On the other hand, displayable dynamic range depends on the gamma correction or tonal curve implied by the image file, or used by the video card and display device. Using a gamma of 2.2 (standard for PC's), it would be theoretically possible to encode a dynamic range of nearly 18 f-stops (see tutorial on gamma correction, to be added). Again though, this would suffer from severe posterization. The only current standard solution for encoding a nearly infinite dynamic range (with no visible posterization) is to use high dynamic range (HDR) image files in Photoshop (or other supporting program).